Red-Black Tree revisited, deleting nodes
Software Development December 22nd, 2008In my last article, I showed how I implemented a red-black tree in C#. One key implementation feature that I left off was the ability to delete a node. The rules for deletion proved to be a little trickier for me than insertion, but I got through it. Before I get into the gritty details of delete, I should at least present the easy alternative. Rather than pulling out nodes and rotating the tree as needed, you could implement a “soft delete”. By this I mean marking a node as deleted, but leaving the tree structure intact. If I were to go this route, I would add a boolean property to the RedBlackNode class to indicate that the node was deleted, and perhaps add an operation to the tree class to rebuild the tree if the number of deleted nodes got too big, something like NodeCount / 2. When the tree was rebuilt, any node that is deleted would not be re-inserted.
This could be implemented fairly easily, and with none of the headache that actually removing the nodes would cause.
1: // The only change to the RedBlackNode class was to
2: // add this auto-property.
3: public Boolean IsDeleted { get; set; }
4:
5: // These are changes/additions to the tree class
6: // This method must be modified to look at the status
7: // of the node
8: public bool Contains(T value)
9: {
10: if (IsEmpty)
11: return false;
12:
13: var current = _rootNode;
14: while (current != null)
15: {
16: switch (value.CompareTo(current.NodeValue))
17: {
18: case -1:
19: current = current.LeftNode;
20: break;
21: case 1:
22: current = current.RightNode;
23: break;
24: default:
25: return !current.IsDeleted;
26: }
27: }
28:
29: // The item wasn't found.
30: return false;
31: }
32:
33: public void DeleteNode(T value)
34: {
35: // Can't delete from an empty tree.
36: if (IsEmpty)
37: return;
38:
39: var current = _rootNode;
40: bool valid = true;
41: while (valid && current != null)
42: {
43: switch (value.CompareTo(current.NodeValue))
44: {
45: case -1:
46: current = current.LeftNode;
47: break;
48: case 1:
49: current = current.RightNode;
50: break;
51: default:
52: SoftDelete(current);
53: valid = false;
54: break;
55: }
56: }
57: }
58:
59: private void SoftDelete(RedBlackNode current)
60: {
61: // Mark the node as deleted.
62: current.IsDeleted = true;
63: _deletedNodes++;
64: _nodeCount--;
65:
66: // Trim the tree if needed.
67: if (_deletedNodes >= _nodeCount / 2)
68: CleanupTree();
69: }
70:
71: private void CleanupTree()
72: {
73: // This will be a list of all non-deleted nodes used to rebuild the tree.
74: var validNodes = new List<RedBlackNode>();
75:
76: // This is how I will make sure I visit every node.
77: var nodeQueue = new Queue<RedBlackNode>();
78: nodeQueue.Enqueue(_rootNode);
79:
80: RedBlackNode current;
81: while(nodeQueue.Count > 0)
82: {
83: current = nodeQueue.Dequeue();
84: // First, add the children of this node to the queue.
85: if (current.LeftNode != null)
86: nodeQueue.Enqueue(current.LeftNode);
87:
88: if (current.RightNode != null)
89: nodeQueue.Enqueue((current.RightNode));
90:
91: // Add the node to the list of valid nodes if it has not been deleted.
92: if (!current.IsDeleted)
93: validNodes.Add(current);
94: }
95:
96: // The queue is empty at this point, so we have visisted every node.
97: // Now we need to rebuild the tree.
98: _rootNode = null;
99: _nodeCount = 0;
100: _deletedNodes = 0;
101: foreach (var node in validNodes)
102: Insert(node.NodeValue);
103: }
104:
You can download the red-black tree implementation using soft delete here.
The alternative to a soft delete is to actually remove the nodes from the tree when they are deleted, which forces us to validate the tree to make sure our rules for a red-black tree are not violated. Deleting a node is more complex than inserting a node. When we inserted a node, we made the inserted node red, so that we only had to deal with double red violations. When a node is deleted, it can be either a red node or a black node. When the node is black, we need to worry about fixing the black node count in the tree so that none of the rules are violated. As a refresher, here were the rules for a red-black tree:
- A red-black tree is a binary search tree, so nodes can have at most 2 children, and any node in the left sub-tree is less than the parent node, while any node in the right sub-tree is greater than the parent node.
- Each node has a color (red or black) and a red node can only have black children. (it is valid for a black node to have black children)
- The number of black nodes from the root node to any leaf contains the same amount of black nodes. This is referred to as the black node count of the tree.
- The root node is always black.
There are a lot of cases for deletion that need to be considered. We’ll start with the easiest ones. The easiest nodes to delete are the leaf nodes of the tree. (those with no children) Even in this simple case there are several scenarios. If the node you deleted is red, you can just remove it from the tree. Since it’s red, the black node count will not be affected in any way, therefore we still have a valid red-black tree. The first case we need to worry about is when we are deleting a black leaf node that has a black sibling (also a leaf node). If we just remove our node, the black node count will be wrong for the tree. This is illustrated in the picture below, where we are deleting the node 15.

When we remove the node from the tree, we have to color the sibling node red and the parent node black to keep the tree valid, otherwise the black count would not be correct. The next scenario is when you are deleting a black leaf node, and the sibling node has 1 child. In this case, rotation is going to be necessary to balance the tree, along with the re-coloring of nodes to keep the tree valid.
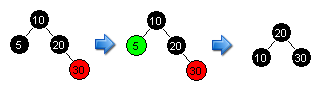
In this case, we are deleting node 5, but to make the tree valid we are going to have to rotate the nodes around the sibling, and color node 30 black. When dealing with this case, we can use the rotation methods that we already developed for insertion to balance the tree. The last case we have to worry about when deleting a black leaf node is when the sibling has 2 children. It turns out that this case is identical to the first case, as shown here:

When determining the rotations, keep in mind that the last 2 cases also have inverses, so there are actually 4 ways that you can end up rotating nodes, depending on where the sibling is in the tree compared to the node being deleted. The most complex case is when we are deleting a black node whose sibling is red with 2 black children, as seen here:
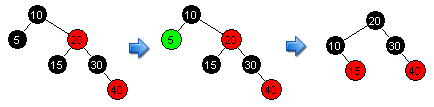
In this case we need to perform rotation to balance the tree, and we also need to recolor nodes. In the situation where the sibling is red with 2 black children, we will often have to perform 2 or 3 rotations to balance the tree again, so this scenario is definitely the most complex.
Now we have covered all the cases when deleting a black leaf node, but what happens when we delete a node that has children? The easy case is when we delete a black node that has a single red child. In this case, we just move the child up and color it black, which makes the tree valid. We can’t have a red node with a single child since that would break the our rules for a red-black tree. Either there would be 2 red nodes in a row, or the black node count would be off.
The last set of scenarios deal with deleting a node that has 2 children. The first thing we need to understand when dealing with this situation is the concept of a successor node. This is critical when deleting nodes from a binary search tree. This node is the one with the closest value to the node in question that is greater than the node. It is easily found in a binary search tree by taking the right child of the node, and then traversing down the left node as far as you can. For example, in the tree below the successor node of the node 20 is the node 28, which is highlighted in green.

The basic concept for deleting a node with 2 children is to find the successor node, pretend that you are deleting that node, and then substituting the successor node in place of the node you deleted. The good news about this is that deleting a successor node will give us a case that we have already dealt with, because the successor is either going to be a leaf node, or a node with a single red child. For example, in the image above, to delete the node 20, we would find the successor, which is 28. Although it’s green in the image, we know from our rules that this node must be a red node, so in effect we are just deleting a red leaf node, which is easy! All we do in this case is replace node 20 with 28, keeping the color the same, and remove the leaf node, making the finished tree look like this:

This is the code I came up with to perform delete:
1: private void HardDelete(RedBlackNode current)
2: {
3: // Make sure we remember to adjust the nodecount.
4: _nodeCount --;
5:
6: if (current.LeftNode != null && current.RightNode != null)
7: {
8: // Find the successor node, swap the value up the tree,
9: // and delete the successor.
10: var successor = FindSuccessor(current);
11: current.NodeValue = successor.NodeValue;
12: PerformHardDelete(successor);
13: }
14: else
15: PerformHardDelete(current);
16: }
17:
18: private void PerformHardDelete(RedBlackNode current)
19: {
20: // The node has either no children or 1 child.
21: if (current.LeftNode == null && current.RightNode == null)
22: {
23: var sibling = GetSiblingNode(current);
24:
25: // In this case we are deleting a leaf node,
26: // just get rid of it.
27: if (current.ParentDirection == Direction.LEFT)
28: current.ParentNode.RightNode = null;
29: else
30: current.ParentNode.LeftNode = null;
31:
32: current.ParentNode = null;
33:
34: // The node is out of the tree, make sure the tree is still valid.
35: // The tree only needs fixed if the node we deleted was black.
36: // If we deleted a red leaf node then nothing needs adjusted.
37: if (current.Color == NodeColor.BLACK)
38: {
39: // If the sibling has no children (it has to be black in this case)
40: if (sibling != null)
41: {
42: if (sibling.LeftNode == null && sibling.RightNode == null)
43: {
44: // Turn the sibling node red to compensate for the
45: // black node being deleted,
46: // and make sure the parent is black.
47: sibling.Color = NodeColor.RED;
48: sibling.ParentNode.Color = NodeColor.BLACK;
49: }
50: else if (sibling.LeftNode == null && sibling.RightNode != null)
51: {
52: // We need to figure out which rotation case fixes the problem.
53: if (sibling.NodeValue.CompareTo(current.NodeValue) > 0)
54: {
55: // There will need to be a rotation to fix this situation, and
56: // nodes will have to be re-colored.
57: sibling.RightNode.Color = NodeColor.BLACK;
58: sibling.Color = sibling.ParentNode.Color;
59: sibling.ParentNode.Color = NodeColor.BLACK;
60: RotateRightChildLeftParent(sibling);
61: }
62: else
63: {
64: // There will be 2 rotations done here, after the first
65: // it becomes the exact same case as above.
66: RotateRightChildRightParent(sibling);
67: sibling.Color = NodeColor.BLACK;
68: sibling.ParentNode.Color = sibling.ParentNode.ParentNode.Color;
69: sibling.ParentNode.ParentNode.Color = NodeColor.BLACK;
70: RotateLeftChildRightParent(sibling.ParentNode);
71: }
72: }
73: else if (sibling.LeftNode != null && sibling.RightNode == null)
74: {
75: // We need to figure out which rotation case fixes the problem.
76: if (sibling.NodeValue.CompareTo(current.NodeValue) > 0)
77: {
78: // There will be 2 rotations done here, after the first
79: // it becomes the exact same case as above.
80: RotateLeftChildLeftParent(sibling);
81: sibling.Color = NodeColor.BLACK;
82: sibling.ParentNode.Color = sibling.ParentNode.ParentNode.Color;
83: sibling.ParentNode.ParentNode.Color = NodeColor.BLACK;
84: RotateRightChildLeftParent(sibling.ParentNode);
85: }
86: else
87: {
88: // There will need to be a rotation to fix this situation, and
89: // nodes will have to be re-colored.
90: sibling.LeftNode.Color = NodeColor.BLACK;
91: sibling.Color = sibling.ParentNode.Color;
92: sibling.ParentNode.Color = NodeColor.BLACK;
93: RotateLeftChildRightParent(sibling);
94: }
95: }
96: else if (sibling.RightNode != null && sibling.LeftNode != null)
97: {
98: if (sibling.Color == NodeColor.BLACK)
99: {
100: if (sibling.NodeValue.CompareTo(current.NodeValue) > 0)
101: {
102: // In this case, the sibling has 2 children.
103: // There will need to be a rotation to fix this situation, and
104: // nodes will have to be re-colored.
105: sibling.RightNode.Color = NodeColor.BLACK;
106: sibling.Color = sibling.ParentNode.Color;
107: sibling.ParentNode.Color = NodeColor.BLACK;
108: RotateRightChildLeftParent(sibling);
109: }
110: else
111: {
112: // In this case, the sibling has 2 children.
113: // There will need to be a rotation to fix this situation, and
114: // nodes will have to be re-colored.
115: sibling.LeftNode.Color = NodeColor.BLACK;
116: sibling.Color = sibling.ParentNode.Color;
117: sibling.ParentNode.Color = NodeColor.BLACK;
118: RotateLeftChildRightParent(sibling);
119: }
120: }
121: else
122: {
123: // This is the case where the sibling of the deleted node is red
124: // with 2 black children.
125: // First, swap the sibling color with the parent color.
126: sibling.ParentNode.Color = NodeColor.RED;
127: sibling.Color = NodeColor.BLACK;
128:
129: if (sibling.NodeValue.CompareTo(current.NodeValue) > 0)
130: {
131: var newSib = sibling.LeftNode;
132: RotateRightChildLeftParent(sibling);
133:
134: if (newSib.Color == NodeColor.BLACK)
135: {
136: // In this case, we need to swap colors to preserve the black node count.
137: if ((newSib.LeftNode == null
138: || (newSib.LeftNode != null
139: && newSib.LeftNode.Color == NodeColor.BLACK))
140: && (newSib.RightNode == null
141: || (newSib.RightNode != null
142: && newSib.RightNode.Color == NodeColor.BLACK)))
143: {
144: newSib.Color = newSib.ParentNode.Color;
145: newSib.ParentNode.Color = NodeColor.BLACK;
146:
147: // Perform additional re-coloring and rotation to fix violations.
148: if (newSib.RightNode != null)
149: newSib.RightNode.Color = NodeColor.BLACK;
150:
151: // Possible case for rotation.
152: if (newSib.Color == NodeColor.RED
153: && (newSib.LeftNode != null || newSib.RightNode != null))
154: RotateRightChildLeftParent(newSib);
155: }
156: else if (newSib.RightNode != null
157: && newSib.RightNode.Color == NodeColor.RED)
158: {
159: // This handles if the new sibling has a red right child.
160: // Perform additional re-coloring and rotation to fix violations.
161: newSib.RightNode.Color = NodeColor.BLACK;
162:
163: newSib.Color = newSib.ParentNode.Color;
164: newSib.ParentNode.Color = NodeColor.BLACK;
165: RotateRightChildLeftParent(newSib);
166: }
167: else if (newSib.LeftNode != null
168: && newSib.LeftNode.Color == NodeColor.RED)
169: {
170: // The new sibling has just a red left child.
171: // Perform additional re-coloring and rotatin to fix violations.
172: RotateLeftChildLeftParent(newSib);
173: newSib.Color = NodeColor.BLACK;
174: newSib.ParentNode.Color = newSib.ParentNode.ParentNode.Color;
175: newSib.ParentNode.ParentNode.Color = NodeColor.BLACK;
176:
177: if (newSib.ParentNode.Color == NodeColor.RED)
178: RotateRightChildLeftParent(newSib.ParentNode);
179: }
180: }
181: }
182: else
183: {
184: var newSib = sibling.RightNode;
185: RotateLeftChildRightParent(sibling);
186:
187: if (newSib.Color == NodeColor.BLACK)
188: {
189: // In this case, we need to swap colors to preserve the black node count.
190: if ((newSib.LeftNode == null
191: || (newSib.LeftNode != null
192: && newSib.LeftNode.Color == NodeColor.BLACK))
193: && (newSib.RightNode == null
194: || (newSib.RightNode != null
195: && newSib.RightNode.Color == NodeColor.BLACK)))
196: {
197: newSib.Color = newSib.ParentNode.Color;
198: newSib.ParentNode.Color = NodeColor.BLACK;
199:
200: // Perform additional re-coloring and rotation to fix violations.
201: if (newSib.LeftNode != null)
202: newSib.LeftNode.Color = NodeColor.BLACK;
203:
204: // Possible case for rotation.
205: if (newSib.Color == NodeColor.RED
206: && (newSib.LeftNode != null || newSib.RightNode != null))
207: RotateLeftChildRightParent(newSib);
208: }
209: else if (newSib.LeftNode != null
210: && newSib.LeftNode.Color == NodeColor.RED)
211: {
212: // Perform additional re-coloring and rotation to fix violations.
213: newSib.LeftNode.Color = NodeColor.BLACK;
214:
215: newSib.Color = newSib.ParentNode.Color;
216: newSib.ParentNode.Color = NodeColor.BLACK;
217: RotateLeftChildRightParent(newSib);
218: }
219: else if (newSib.RightNode != null
220: && newSib.RightNode.Color == NodeColor.RED)
221: {
222: // The new sibling has just a red left child.
223: // Perform additional re-coloring and rotatin to fix violations.
224: RotateRightChildRightParent(newSib);
225: newSib.Color = NodeColor.BLACK;
226: newSib.ParentNode.Color = newSib.ParentNode.ParentNode.Color;
227: newSib.ParentNode.ParentNode.Color = NodeColor.BLACK;
228:
229: if (newSib.ParentNode.Color == NodeColor.RED)
230: RotateLeftChildRightParent(newSib.ParentNode);
231: }
232: }
233: }
234: }
235: }
236: }
237: }
238: }
239:
240: if (current.LeftNode != null)
241: {
242: // In this case, the node we are deleting has a single child, so we know it's a
243: // black node. A red node can't have a single child because it wouldn't be a
244: // valid tree.
245: current.LeftNode.ParentNode = current.ParentNode;
246:
247: // This shouldn't happen since we checked for the root node above
248: // but resharper warnings annoy me
249: if (current.ParentNode != null)
250: {
251: if (current.ParentDirection == Direction.LEFT)
252: current.ParentNode.RightNode = current.LeftNode;
253: else
254: current.ParentNode.LeftNode = current.LeftNode;
255: }
256: }
257:
258: if (current.RightNode != null)
259: {
260: // In this case, the node we are deleting has a single child, so we know it's a
261: // black node. A red node can't have a single child because it wouldn't be a
262: // valid tree.
263: current.RightNode.ParentNode = current.ParentNode;
264:
265: // This shouldn't happen since we checked for the root node above
266: // but resharper warnings annoy me
267: if (current.ParentNode != null)
268: {
269: if (current.ParentDirection == Direction.LEFT)
270: current.ParentNode.RightNode = current.RightNode;
271: else
272: current.ParentNode.LeftNode = current.RightNode;
273: }
274: }
275: }

December 22nd, 2008 at 4:30 pm
Sedgewick has fine-tune red-black trees and has a paper on left-leaning red-black trees (released earlier this year).
http://www.cs.princeton.edu/~rs/talks/LLRB/LLRB.pdf
The basic idea is to eliminate the case where the right child is red and the left child is black (using the existing rotation mechanism). This simplifies the code to do inserts and deletes while preserving the time complexity.
If you try the techniques in the paper, I think you’ll find your code gets simpler.
December 22nd, 2008 at 4:34 pm
That’s an interesting paper, I didn’t come across that while I was working on this. I’ll have to dig into it. Thanks for the link!
February 1st, 2009 at 4:23 pm
Thx, very good explaination and illustration about deleting a black leaf in RBT (i think this is a only web-site with that kind of explanation – its better explained than on Wikipedia)
August 22nd, 2009 at 2:07 pm
[...] von Hilfsknoten (”NIL”) und Referenzierung der Mutterknoten verkompliziert. Eine komplette Implementierung der delete-Methode ist sowieso nur schwer zu finden. Auch in der ursprünglichen [...]
October 19th, 2009 at 10:32 am
I think the method PerformHardDelete has a bug. It does not consider the case when the node being deleted is the root (i.e. the only last node). Then it gives null reference exception at
if (current.ParentDirection == Direction.LEFT)
–>>> current.ParentNode.RightNode = null;
else
I will need to make a closer look if explicit check will solve the problem.
October 23rd, 2012 at 1:21 pm
Download appears to be broken. Also, what license are you releasing this under? I’d like to alter this for use in my own (open-source) project.
April 20th, 2013 at 7:28 pm
Ferad is right, there is a bug: the method PerformHardDelete does not consider the case when the node being deleted is the root
April 21st, 2013 at 5:17 pm
Sorry, it does work OK!
In line 11: current.NodeValue = successor.NodeValue;
This didn’t work because NodeValue was private. Once I changed it to public (and added set{} to the constructor) the root node was deleted correctly!
Thank you Jack Altiere!
October 29th, 2014 at 6:48 pm
ケイトスペード バッグ エナメル…
The United States on February 9″daily” financial network China has an aircraft carrier is building a second aircraft carrier,In the case of budget cuts it is an attractive proposalAlthough the Chinese navy since the 1970 s had great progress,China ha…